Welcome to Perceptron, part of our Neural Networks series.

When you think about ANN, RNN, CNN, FNN, GAN, LSTM, and so on, remember, that this is the base of all your ANN, so you can easily go through the slides with a realistic scenario of a perceptron. One of the simplest yet most fundamental artificial neural network architectures. If you’re just getting started with AI, understanding the perceptron is a great way to build your foundation in neural networks.

What is a Perceptron?

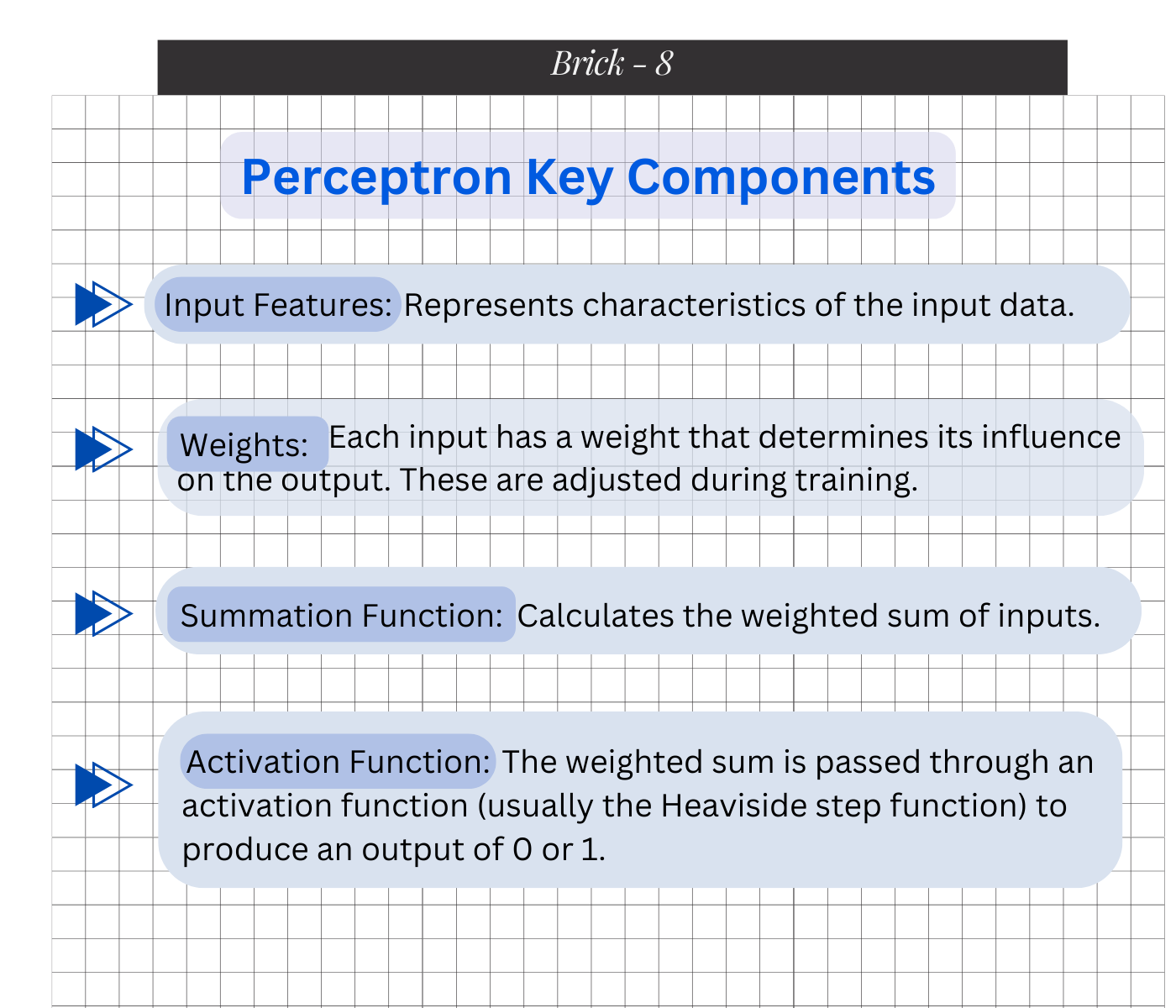
The perceptron is an algorithm for supervised learning of binary classifiers. It’s a type of linear classifier, i.e., a classification algorithm that makes its predictions based on a linear predictor function combining a set of weights with the feature vector.

Historical Background

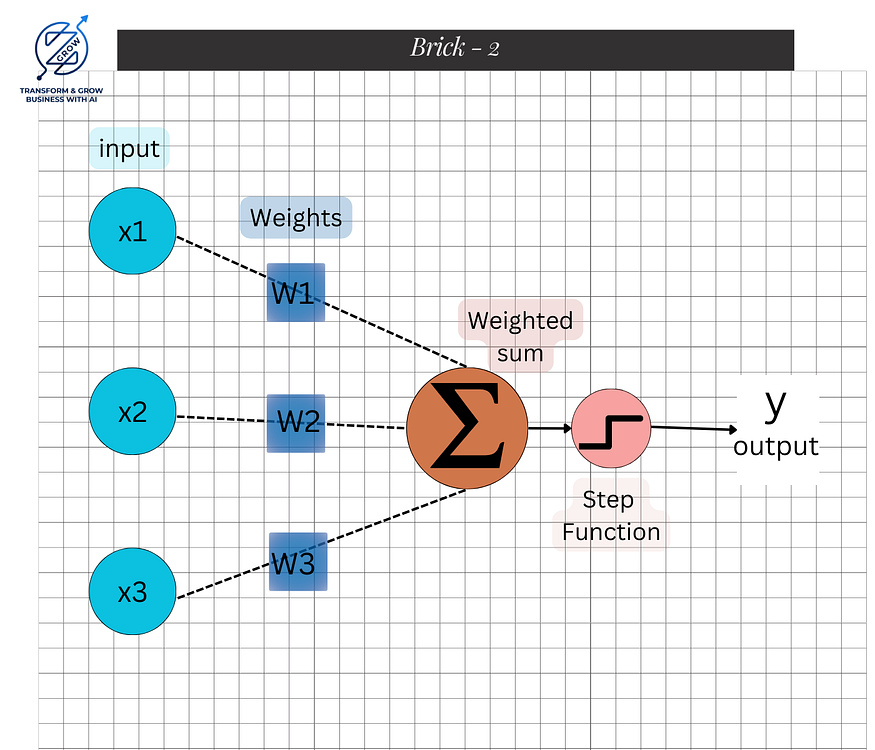
The perceptron was introduced by Frank Rosenblatt in 1957. It represents the simplest type of feedforward neural network, consisting of a single layer of input nodes that are fully connected to a layer of output nodes. This basic structure makes it a powerful tool for understanding the principles behind more complex neural network models.

Structure of a Perceptron

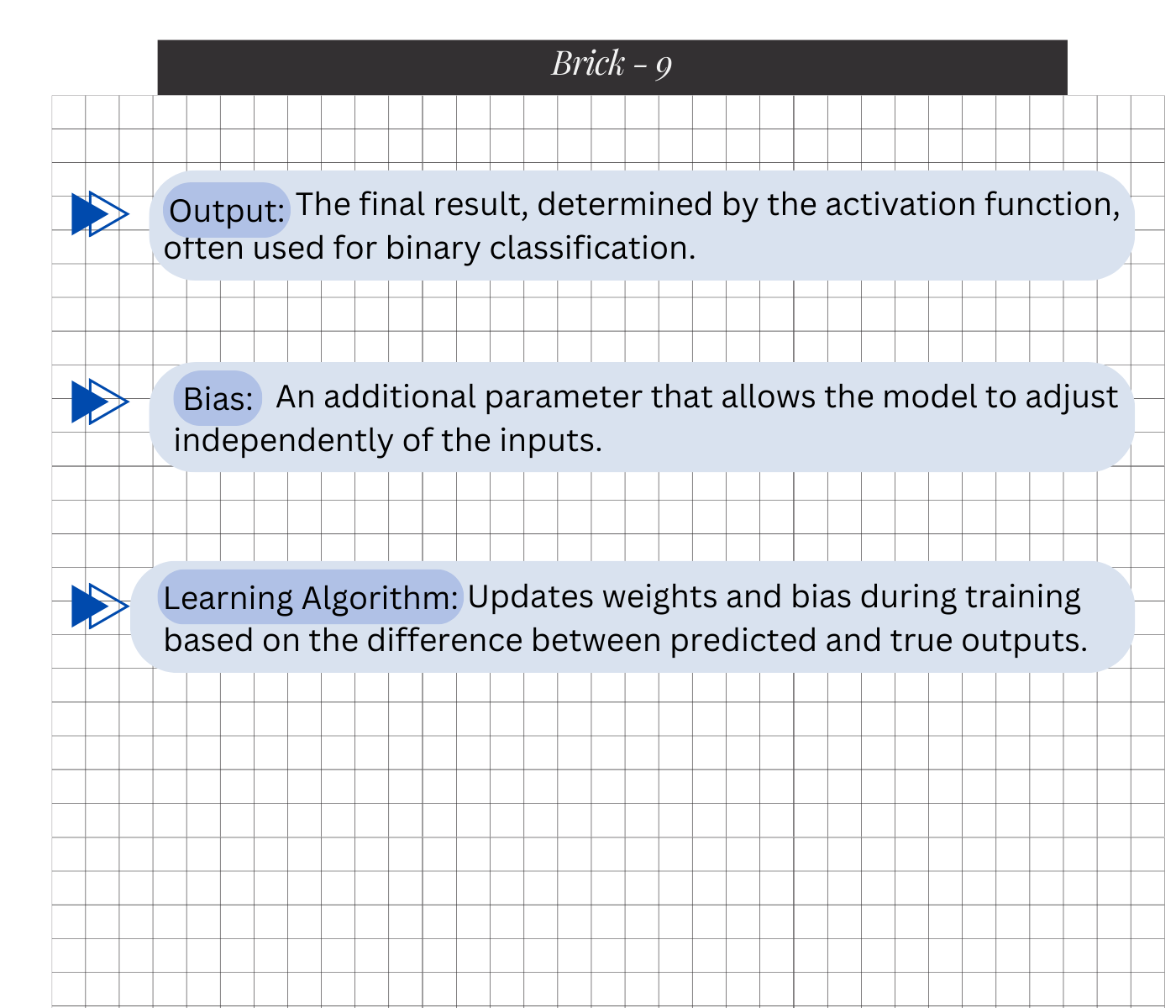
A perceptron consists of:

• Input Layer: The layer where the perceptron receives the input data. Each node in this layer represents an input feature.
• Weights: Each input is assigned a weight, which is adjusted during the training process.
• Summation Processor: The weighted inputs are summed together.
• Activation Function: The sum of the weighted inputs is passed through an activation function to produce the output. The most commonly used activation function in a perceptron is the step function.
  
  
  

How Does a Perceptron Work?

1. Initialization: Start with random weights.
2. Input: Receive input features.
3. Weighting: Multiply each input feature by its corresponding weight.
4. Summation: Sum all the weighted inputs.
5. Activation: Pass the sum through an activation function to determine the output.
6. Learning: Adjust the weights based on the error in the output.

Learning Rule

The perceptron learning rule is simple yet effective. It updates the weights in proportion to the error between the predicted output and the actual output: Δwi=η(y−y^)xi\Delta w_i = \eta (y — \hat{y}) x_iΔwi​=η(y−y^​)xi​ where η\etaη is the learning rate, yyy is the actual output, y^\hat{y}y^​ is the predicted output, and xix_ixi​ is the input feature.

Realtime scenario exposition:

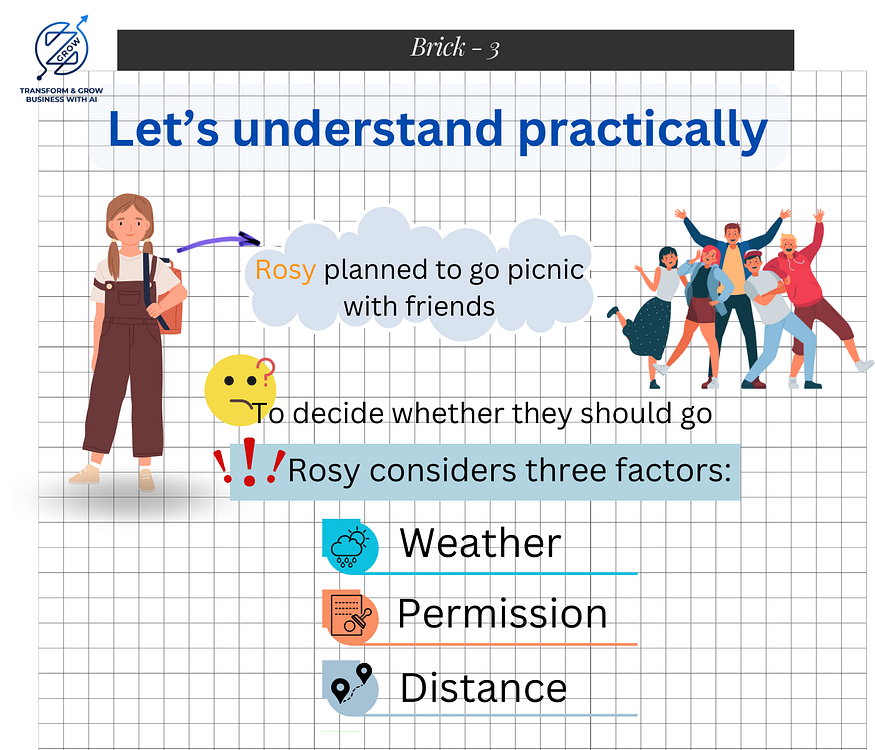
Meet Rosy, who is planning to go on a picnic with her friends. To decide whether they should go, Rosy considers several factors (features) before making a decision:

1. Weather
2. Permission
3. Distance

Rosy assigns importance (weights) to each factor:

• Weather: 4
• Permission: 2
• Distance: 2
  
  

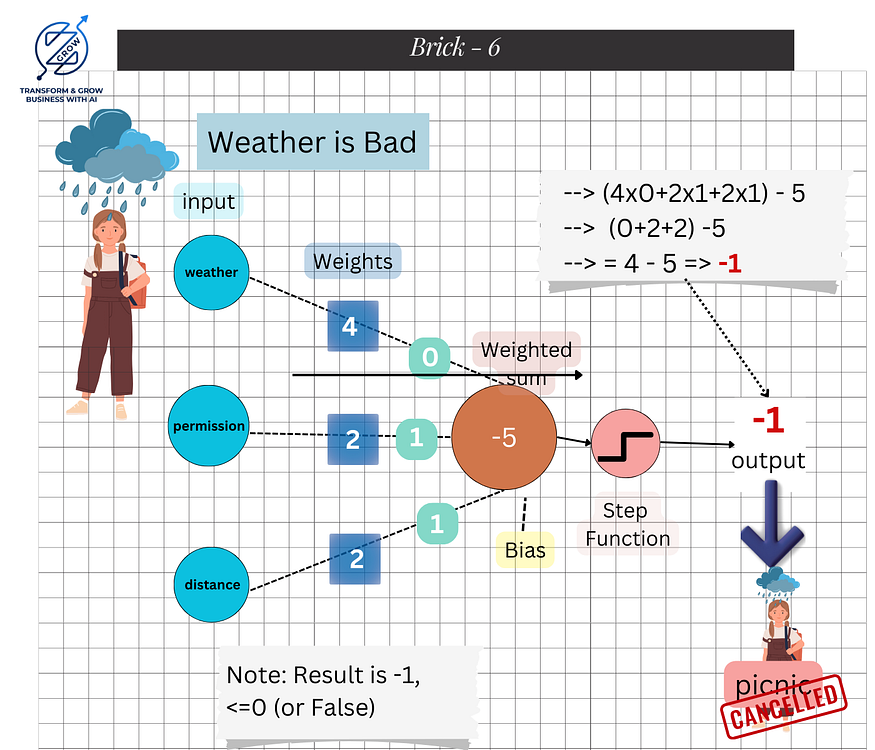
The weather is the most critical factor, so it gets the highest weight. Here’s how Rosy makes her decision:

1. Weather Condition: Bad (0) or Good (1)
2. Permission: Granted (1) or Not Granted (0)
3. Distance: Near (1) or Far (0)

Let’s see how Rosy uses these factors to decide about the picnic:

• If the weather is bad (0), permission is granted (1), and the distance is near (1), the calculation goes like this: Total Score=(4×0)+(2×1)+(2×1)=4\text{Total Score} = (4 \times 0) + (2 \times 1) + (2 \times 1) = 4Total Score=(4×0)+(2×1)+(2×1)=4

Rosy also has a bias (threshold) of 5. To decide:

• Subtract the bias from the total score: 4−5=−14–5 = -14−5=−1

If the result is less than or equal to 0, they won’t go on the picnic. Since the result is -1, Rosy decides not to go on the picnic.

This story illustrates the basic idea behind a perceptron:

• Inputs: Weather, Permission, Distance
• Weights: Importance of each factor
• Bias: Threshold for making the decision
  
  

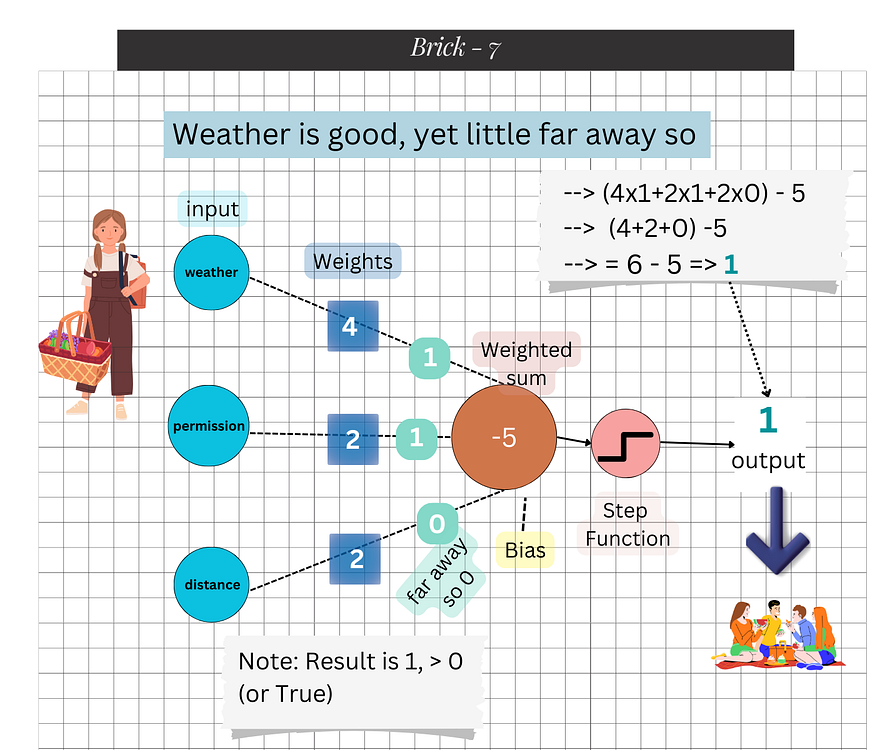
By understanding this simple story, you get the essence of how a perceptron works to make binary decisions.

Applications of Perceptron

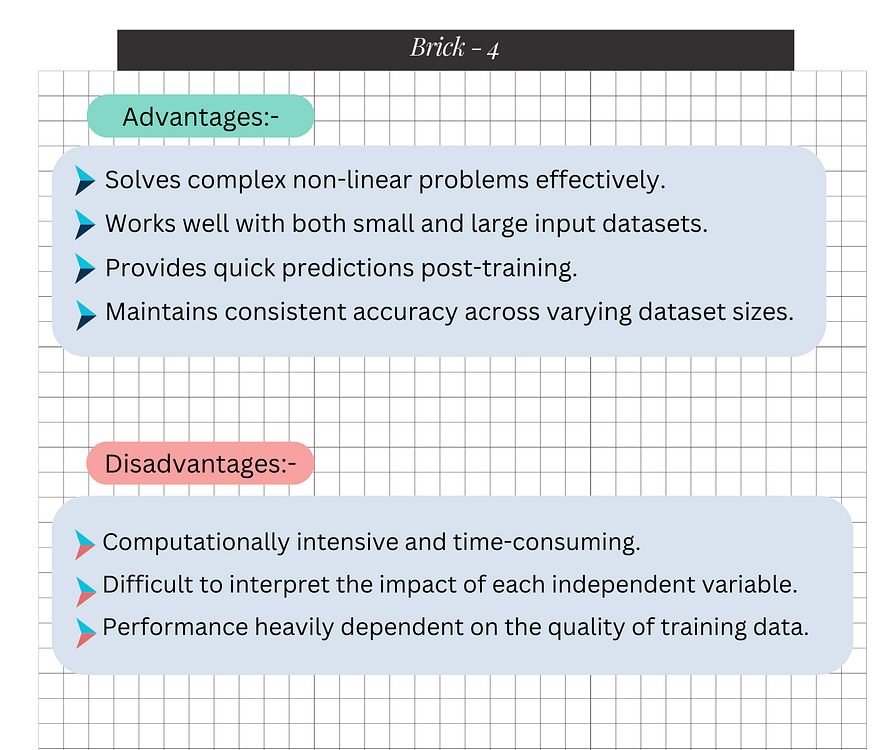
Despite its simplicity, the perceptron is powerful for solving linearly separable problems. It laid the groundwork for the development of more complex neural network architectures and algorithms. Some applications include:

• Binary Classification: Determining whether an email is spam or not.
• Pattern Recognition: Identifying simple patterns within data.

Limitations

While the perceptron is an important concept in neural network theory, it has its limitations. The most significant is that it can only solve problems that are linearly separable. This means it struggles with more complex, non-linear data.

Conclusion

The perceptron may be simple, but it’s a crucial stepping stone in the world of neural networks and AI. Understanding its workings helps in grasping more advanced concepts in neural networks and deep learning.

We hope this post provided you with a clear and concise overview of the perceptron. Stay tuned for our next post, where we will delve deeper into more complex neural network architectures.

No need to memorize words, just understand the concept.
Enjoy learning about perceptrons through our picnic trip example, and stay tuned for more!

Happy learning with building bricks.

Follow us for more insights!

Build the foundation with the next step of innovations.

#neuralnetwork #ArtificialIntelligence #GENAI #GenerativeAI #perceptron #Technology #Future #AITrends #Fundamentals #Algorithm